
Pistacchio arrives home after a night of debauchery, in which he began by toasting with a 1959 Dom Perignon Rosé and ended by making a white background with Bardahl tractor antifreeze.
Upon reaching the door of his residence, he extracts the bunch of 10 indistinguishable keys (at least in his condition) and thinks: If I randomly choose the keys one by one and try… in which attempt do I have the most probability of finding the correct key? ?
Scroll down to see the answer!
You may be surprised to learn that the answer is on the first try.
The probability that you use the correct key on the first try is 1/10.
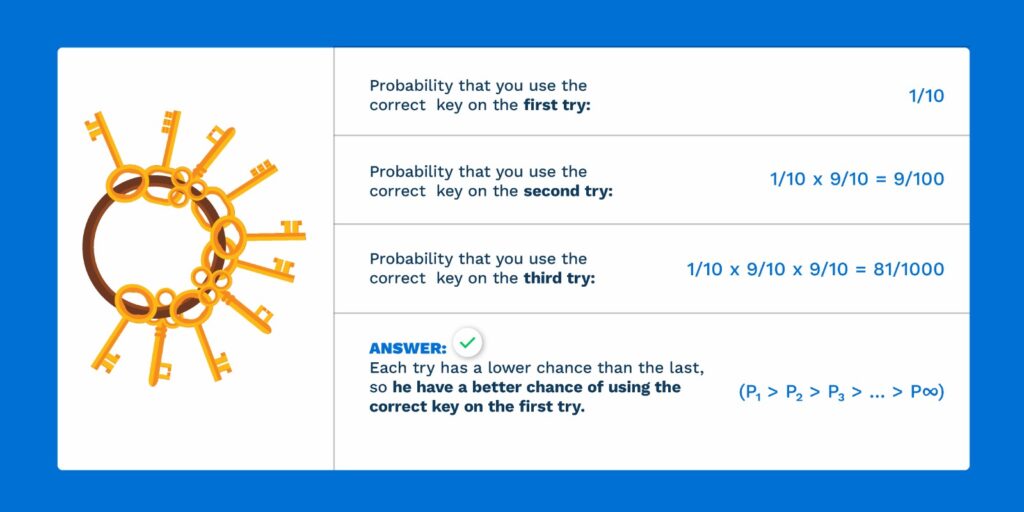
The probability that you use the correct key on the second try is 1/10, multiplied by the probability that you could not open the door on the first try, that is, times 9/10. We have to keep in mind that he only has a 9/10 chance of making it on the second try.
The probability that you use the correct key on the third try is 1/10, multiplied by the probability that you could not open the door on the first try or on the second try.
Each try has a lower chance than the last, so you have a better chance of using the correct key on the first try.

